HOME»データベーススペシャリスト令和2年秋期»午前Ⅰ 問2
データベーススペシャリスト令和2年秋期 午前Ⅰ 問2
問2
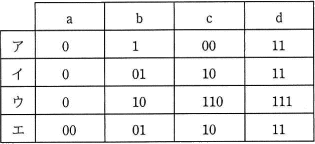
a，b，c，d の4文字から成るメッセージを符号化してビット列にする方法として表のア～エの4通りを考えた。この表は a，b，c，d の各1文字を符号化するときのビット列を表している。メッセージ中の a，b，c，d の出現頻度は，それぞれ，50%，30%，10%，10% であることが分かっている。符号化されたビット列から元のメッセージが一意に復号可能であって，ビット列の長さが最も短くなるものはどれか。
- [出典]
- 応用情報技術者
令和2年秋期 問4と同題
分類
テクノロジ系 » 基礎理論 » 情報に関する理論
正解
ウ
解説
最小ビットで圧縮できる方式を考える前に、各方式が符号化されたビット列から元のメッセージを一意に復号可能かどうかを検証し、条件を満たす方式についてだけビット数を計算します。
- 符号化後のビット列に"11"があった場合、bb(11)とd(11)の区別がつかないので、元のメッセージに一意に復号することができません。
- 符号化後のビット列に"00110"があった場合、abc(00110)とaada(00110)の区別がつかないので、元のメッセージに一意に復号することができません。
- 一意の復号が可能です。各文字の出現頻度を考慮すると、1文字を表現するのに必要な平均ビットは、
(1×0.5)＋(2×0.3)＋(3×0.1)＋(3×0.1)
＝0.5＋0.6＋0.3＋0.3＝1.7
となり、4つの中では復号可能かつビット列の長さが最も短くなる方法となります。 - 各文字が2ビットずつなので一意の復号が可能です。
1文字を表現するのに必要な平均ビットは2ビットなので、「ウ」の方式よりはビット列が長くなります。