HOME»データベーススペシャリスト令和3年秋期»午前Ⅰ 問1
データベーススペシャリスト令和3年秋期 午前Ⅰ 問1
問1
非線形方程式 ƒ(x)=0 の近似解法であり,次の手順によって解を求めるものはどれか。ここで,y=ƒ(x) には接線が存在するものとし,(3)でx0と新たなx0の差の絶対値がある値以下になった時点で繰返しを終了する。
〔手順〕
〔手順〕
- 解の近くの適当なx軸の値を定め,x0とする。
- 曲線 y=ƒ(x) の,点(x0,ƒ(x0))における接線を求める。
- 求めた接線と,x軸の交点を新たなx0とし,手順(2)に戻る。
- オイラー法
- ガウスの消去法
- シンプソン法
- ニュートン法
分類 :
テクノロジ系 » 基礎理論 » 応用数学
正解 :
エ
解説 :
- オイラー法は、常微分方程式の数値的解法の一つで、初期値である点(x0,ƒ(x0))における接線を求め、その接線の傾きと十分に小さい刻み幅hを用いて x1=x0+h、x2=x1+h、…における y(x) の順次求めていくことで近似値を得る方法です。
- ガウスの消去法(掃き出し法)は、行列表現を用いて、前進消去と後退代入という2つのステップで連立一次方程式などを解くための方法です。
- 数値積分法の一つで、非線型方程式の3点を通る二次関数で各区間を近似することで、2点を使う台形公式よりも高精度の近似値を求める方法です。
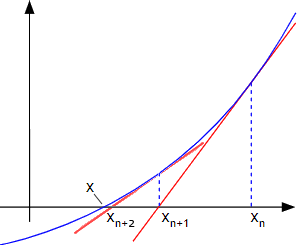
- 正しい。ニュートン法は、微分方程式の解の一つを求める方法で、任意に定めた解の予測値から始めて、接線とx軸の交点を求める計算を繰り返しながら、その値を ƒ(x) = 0 となるxに近づけていく方法です。計算前のxと計算後のxの差が設定した誤差の範囲になるまで計算を繰り返します。
出典
- 応用情報技術者令和3年秋期 問1と同題
